令和4年度試験問題 問43
問43解説へ
図のアローダイアグラムにおいて,作業Bが2日遅れて完了した。そこで,予定どおりの期間で全ての作業を完了させるために,作業Dに要員を追加することにした。作業Dに当初20名が割り当てられているとき,作業Dに追加する要員は最少で何名必要か。ここで,要員の作業効率は一律である。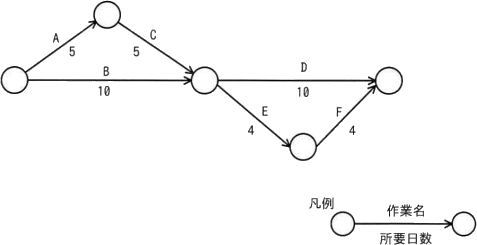

- 2
- 3
- 4
- 5
正解 エ問題へ
広告
解説
まず設問のアローダイアグラムにおけるクリティカルパスを考えます。
作業Bが2日遅れたということは、作業Bの完了までに要した日数は12日ということになります。よって、工程全体を20日で完了するためには作業Dを8日で終えなくてはなりません。もともと20人で10日掛かっていた作業を8日で完了させるために必要な要員数は、以下のように求めることができます。
10日×20人=200人日
200人日÷8日=25人
作業Dに当初割り当てられていた要員数は20人なので、最少追加人数は「25-20=5名」となります。
【別解】
10人で行っていた作業を8人で同日数で完成させるためには、
8×n=10
n=1.25
より、1日当たり1.25倍の作業をこなす必要があります。要員の作業効率は一律なので単純に従前より1.25倍の要員が必要となります。
20人×1.25=25人
25人-20人=5人
- A→C→D
- 5+5+10=20日
- A→C→E→F
- 5+5+4+4=18日
- B→D
- 10+10=20日
- B→E→F
- 10+4+4=18日
作業Bが2日遅れたということは、作業Bの完了までに要した日数は12日ということになります。よって、工程全体を20日で完了するためには作業Dを8日で終えなくてはなりません。もともと20人で10日掛かっていた作業を8日で完了させるために必要な要員数は、以下のように求めることができます。
10日×20人=200人日
200人日÷8日=25人
作業Dに当初割り当てられていた要員数は20人なので、最少追加人数は「25-20=5名」となります。
【別解】
10人で行っていた作業を8人で同日数で完成させるためには、
8×n=10
n=1.25
より、1日当たり1.25倍の作業をこなす必要があります。要員の作業効率は一律なので単純に従前より1.25倍の要員が必要となります。
20人×1.25=25人
25人-20人=5人
広告