ITパスポート 試験情報＆徹底解説

用紙サイズ同士は相似形であり、用紙サイズが1つ小さくなるごとに用紙の面積が半分になる関係があります。辺の長さを見てみると、A4判の長辺はA3判の短辺と同じ、A4判の短辺はA3の長辺の半分の長さになっています。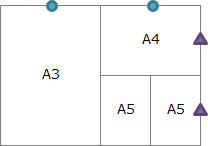A4判の長辺を"1"、A3判の長辺を"x"とすると、各辺の長さは以下のように表すことができます。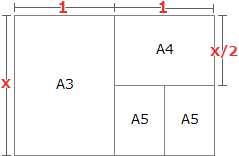A3判とA4判で短辺：長辺の比率は変わらないので、2組の辺の長さの比率を比例式にすると、

　x：1＝1：x/2
　x²/2＝1
　x²＝2
　x＝2≒1.41

以上より、A3判の長辺はA4判の長辺の約1.41倍になることがわかります。したがって「ア」が正解です。

【別解】
A3判の長辺はA5判の長辺の2倍の長さになっています。A5→A4、A4→A3で長辺の倍率は同じはずなので、用紙サイズが1つ大きくなるときの長辺の倍率を"n"とすると、A4判の長辺はA5判の長辺のn倍、A3判の長辺はA5判の長辺のn²倍になります。この関係を式に表すと、

　1×n×n＝2
　n²＝2
　n＝2≒1.41